California and New York Schools' Bar Pass Rates and Linearity
Over at Empirical Legal Studies, Bill Henderson picked up on my analysis of the relationship between law schools’ LSAT midpoint (taken from the 2007 US News law school rankings study and calculated as the average of the 25th and 75th percentiles) and their average pass percentage on the California Bar examination (Pearson r = .90). Based on the diagram I posted, he pointed out that the relationship was nonlinear; that was primarily because of three schools at the lower end of the distribution. In part Bill used the discussion of bar pass rate as a case study in the importance of "eye balling" the data.
Bill did not have the actual data, so he worked from my scatterplot to draw a line that seemed to best fit the data points. Here is another plot showing a quadratic fit calculated from the data. It is remarkably similar to the line Bill drew. The correlation coefficient is .93.
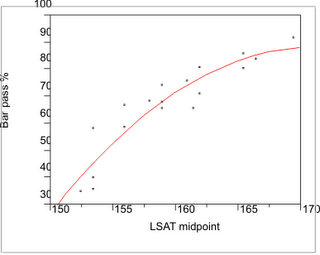I initially thought about excluding the three pertinent schools as outliers (not usually a good idea, especially if you don't have many observations to begin with, and also because it may result in missing important features of a relationship such as nonlinearity). But when the three schools are excluded, the relationship for the remaining 15 schools appears essentially linear (Pearson r = .92).
As Bill commented, his thread on this topic “is invoking some pretty high-end modeling concepts,” and I won’t attempt to deal with those. The relationship between the LSAT and New York bar pass percentages provided by US News for 22 schools is, however, worth another look in this context. Here is a plot of the data showing a relationship that appears to be linear (Pearson r = .92.)
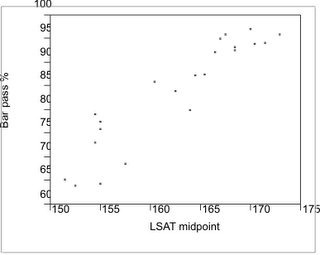Seven of the 22 schools are located outside New York state. They are an elite group: Duke, George Washington, Georgetown, Michigan, NYU, Penn, and Yale. Their bar pass percentage (M = 93.39, SD = 3.01) was significantly greater than that of the 17 New York schools (M = 79.18, SD = 10.87; t test for unequal variances = 4.69, df = 17.84, p < .0002). The latter schools include both elites and lower ranked schools. As is apparent from their bar-pass standard deviation, their graduates had a wide range of average success on the bar examination.
Alfred L. Brophy
Bill did not have the actual data, so he worked from my scatterplot to draw a line that seemed to best fit the data points. Here is another plot showing a quadratic fit calculated from the data. It is remarkably similar to the line Bill drew. The correlation coefficient is .93.
I initially thought about excluding the three pertinent schools as outliers (not usually a good idea, especially if you don't have many observations to begin with, and also because it may result in missing important features of a relationship such as nonlinearity). But when the three schools are excluded, the relationship for the remaining 15 schools appears essentially linear (Pearson r = .92).As Bill commented, his thread on this topic “is invoking some pretty high-end modeling concepts,” and I won’t attempt to deal with those. The relationship between the LSAT and New York bar pass percentages provided by US News for 22 schools is, however, worth another look in this context. Here is a plot of the data showing a relationship that appears to be linear (Pearson r = .92.)
Seven of the 22 schools are located outside New York state. They are an elite group: Duke, George Washington, Georgetown, Michigan, NYU, Penn, and Yale. Their bar pass percentage (M = 93.39, SD = 3.01) was significantly greater than that of the 17 New York schools (M = 79.18, SD = 10.87; t test for unequal variances = 4.69, df = 17.84, p < .0002). The latter schools include both elites and lower ranked schools. As is apparent from their bar-pass standard deviation, their graduates had a wide range of average success on the bar examination.Alfred L. Brophy
posted by Alfred Brophy at 3:21 PM
1 Comments:
Well, according to your analysis, I have about a 70% chance of passing the bar. Since that's about a 20% better chance than I gave myself, I like it!
Post a Comment
<< Home