Practical advice for new law professors: Grading on a curve

Around this time of year, American law schools begin issuing offers for entry-level, tenure-track teaching positions. The typical new recruit has more experience with scholarship than with teaching, grading, or lesson-planning. MoneyLaw will offer some practical advice to some of these new law professors. I will start by explaining standard scoring, more colloquially known as grading on a curve.

Why? At a minimum, this forum takes some pleasure in indulging the holiday spirit of giving and sharing. More seriously, I am acutely aware that many American lawyers — and many of their teachers — tend to be innumerate. With regrettable frequency over the course of nearly two decades in the legal academy, I have heard tenured law professors assert that "there is no mechanical way to convert raw scores to scaled grades." The truth is much simpler: There is a set of practical problems that mathematics can solve. Standard scoring is one of them. Instead of being content to post the occasional exercise in refreshing my own quantitative skills, I will try to share a few things with newcomers to the academy — ideally, things not discussed at the law school hiring combine or during faculty orientation.

Most (though not all) American law schools enforce some form of constraint on the grades that their professors can assign. Wikipedia has collected a list of grade point average curves at American law schools. The subject arises with regularity in prelaw and law student blogs, and with good reason. Some law schools condition their students' retention of financial aid on the maintenance of a minimum GPA. If you know the mathematics of standard scoring, you can predict with a high degree of accuracy the probability of maintaining the threshold GPA throughout all three years of law school. Students and professors alike therefore have a stake in understanding the mathematics of grading.

Read the rest of this post . . . .In my experience, law professors who react instinctively, and perhaps even inanely, against grading on a curve do so for either or both of two reasons. One is simple ignorance, a byproduct of the innumeracy that might have prompted them to study law instead of a more quantitatively demanding discipline. The other is an inborn distrust of authority. That distrust often extends to school-wide rules on mean GPAs or grade distributions, as though divining the precise line between a C+ and a B- represented a central plank of academic freedom. The truth is that standard scoring leaves ample discretion for all instructors to evaluate their students and to distribute individual grades. The only constraint is that the mean grade in each course should fall within some range. (How tight that range should be, like almost every other subject imaginable, is the subject of some dispute among law professors.). Moreover, the exercise of "grading on a curve" is both mathematically elegant and logistically simple. You have no excuse for not grading on a curve.

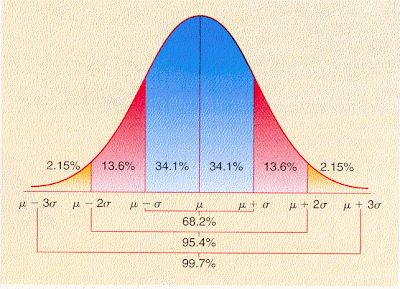
Absent extraordinary circumstances, grades in any class will follow a normal, Gaussian distribution. Happily, grading a class means measuring an entire population. We can therefore use standardization techniques.

I will further assume, for clarity's sake, a straightforward map of points corresponding to letter grades. In increments of 0.333, progress from 0.000 for an F to 4.333 for an A+. In other words, a C+ is worth 2.333. A B- is worth 2.667. Many schools use no more than one significant digit after the decimal point, which leads to mathematical anomalies arising from crude rounding. At 2.3, a C+ is 0.3 points removed from a C, but 0.4 points removed from a B-.

Finally, I assume that the professor consistently adheres to some way, any way of assigning raw scores. Giving points for each valid argument and assigning percentages for each task accomplished represent merely two among many plausible methodologies. The real trick lies in converting these raw scores to standard scores.

Begin by calculating the z-score. The z-score, or simply z, may be computed according to this formula:

z = (x – μ) / σ



Where:

x  =  Raw score to be standardized
μ  =  Mean raw score
σ  =  Standard deviation

In practice, most values of z will be greater than -2 and less than 2. Absolute values of z exceeding 2 correspond to true outliers, and those students are either ironclad locks for the book award, or good candidates for receiving an F. In my own career, I have issued F's very sparingly because the D and D- minus grades carry roughly the same message without automatically depriving a student of academic credit. Generally speaking, if |z| > 2, I counsel removing the grade in question from the curving algorithm I am about to describe and assigning it "manually," after careful comparison to the other student performances that are closest to it.

If the target class mean is a C+, or 2.333, and the instructor is willing to stretch the distribution of grades from a dummy grade of F+ (0.333, or 2.333 - 2, as the midpoint between an F at 0.000 and a D- at 0.667), to A+ (4.333, or 2.333 + 2), then each student's grade can be very simply calculated:

g = 2.333 + z

This example works because it a special case, with very easy figures, of the more general formula for standardizing a set of normally distributed raw scores:

g = K + z * (M – K) / 2

Where:

g  =  Scaled grade
z  =  The z-score (standardized score) as defined above
K  =  Target class mean
M  =  Maximum grade point value, typically 4.333 in a system with an A+

The denominator in the final fraction, or 2, reflects the maximum absolute value of z that we realistically expect to encounter in this population. It would not be inappropriate to adjust this denominator slightly upward to catch not just most but all scores we expect to fall between the first and 99th percentiles. Nor is it inappropriate for an instructor to give close personal attention to exams whose z-scores approach -2. In the absence of a true F+ grade, a scaled grade of 0.333 invites discretion to choose between an F and a D- (or a D in universities that have abolished the grade of D-).

Substituting 2.333 for K and 4.333 for M yields the simpler formula above.

Recall my earlier observation that most (though not all) z-score values will fall between -2 and 2. In other words, -2 ≤ z ≤ 2 in most instances. If you divide the z-score range from -2 to 2 into equal bands of 0.5, and you envision all z-scores below -2 and all z-scores above 2 as bands of their own, you will find 10 zones corresponding very nicely to the 10 passing grades from D+ to A+, inclusive:

Minimum z-score	Letter grade
<-2.0	D+ (or lower, in truly extreme cases)
-2.0	C-
-1.5	C
-1.0	C+
-0.5	B-
0.0	B
+0.5	B+
+1.0	A-
+1.5	A
+2.0	A+

The closely related system of stanines (Standard Nines) also works very well with the grading scale I have just described. The United States military historically valued stanines as a way of translating the z-scores of standard scoring, which range across either side of zero, to a scale of single-digit integers from 1 to 9 inclusive. To use stanines, divide a Gaussian distribution into nine bands, centered on the fifth band. The second through eighth bands each traverse 0.35 standard deviations; the first and ninth stanine cover, respectively, the lowest and highest ends of the distribution. Assigning a B- (2.667) to the fifth stanine and moving one-third of a letter grade in each direction yields the following table of converted grades:

Stanine	Letter grade
1	D+ (or lower, in truly extreme cases)
2	C-
3	C
4	C+
5	B-
6	B
7	B+
8	A-
9	A (or A+, for truly outstanding performances)

As a final bonus, faithful readers of this forum will recognize that z-scores lie at the heart of the U.S. News rankings of law schools and other branches of American universities. Demystifying standard scoring in the classroom represents a modest but important first step toward demystifying one magazine's standard scores of competing classrooms.